Louis de Broglie's "mechanical analogy" for de Broglie vibrations and wavelengthDe Broglie's original paper (his thesis actually) is seldom read for two reasons:
Most people do not realize that de Broglie vibration is the funcamental parameter, and that:
- de Broglie "waves" are an artifact of the effect of the Lorentz transform on time, creating clock skew, even at slow speeds
- de
Broglie "frequency" really does transform in the ordinary relativistic
way, but it seems higher because we observe the spatially distributed
wave, i.e. we are looking at an array of clocks, not just one clock.
De
Broglie gave a verbal description of a "mechanical analogy" of his
waves. The purpose of this web page is to present animated
drawings of this description for stationary and moving particles.
For further information, you can view a pre-review copy of a
paper on
Common pedagogical issues with de Broglie waves: moving double slits, composite mass and clock synchronization. To view the animations, click on one of the images below. De Broglie's description:
Our theorem teaches us, moreover, that
this wave represents a spacial distribution of phase, that is to say, it is a
"phase wave." To make the last point more precise, consider a
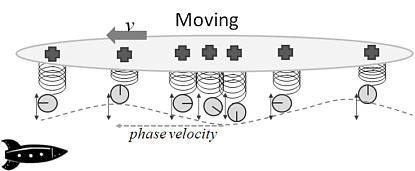
mechanical comparison, perhaps a bit crude, but that speaks to one's
imagination. Consider a large, horizontal circular disk, from which identical
weights are suspended on springs. Let the number of such systems per unit area,
i.e., their density, diminish rapidly as one moves out from the centre of the
disk, so that there is a high concentration at the centre. All the weights on
springs have the same period; let us set them in motion with identical
amplitudes and phases. The surface passing through the centre of gravity of the
weights would be a plane oscillating up and down. This ensemble of systems is a
crude analogue to a parcel of energy as we imagine it to be. 
This page (c) 2015 by Robert Shuler - home - papers

